
문제

위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록solution 함수를 완성하세요.
제한사항
삼각형의 높이는 1 이상 500 이하입니다.
삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력 예
| triangle | result |
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
코드
class Solution {
public int solution(int[][] triangle) {
int answer = 0;
int N = triangle.length;
int M = triangle[N-1].length;
int[][] dp = new int[N][M];
dp[0][0] = triangle[0][0];
for(int i = 0; i < N-1; i++){
for(int j = 0; j < triangle[i].length; j++){
for(int k = j; k < j+2; k++){
int num = dp[i][j] + triangle[i+1][k];
dp[i+1][k] = Math.max(dp[i+1][k], num);
}
}
}
for(int i = 0; i < M; i++){
answer = Math.max(answer, dp[N-1][i]);
}
return answer;
}
}
풀이
이 문제를 왜 DP로 풀어야 하나요?!
문제 분류가 DP 이기 때문에?
뭐 솔직히 그것도 맞긴한데
이걸 dsp로 푼다고 해봅시다.
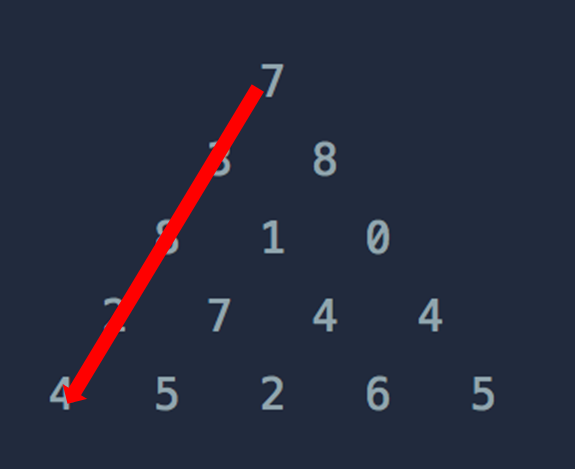
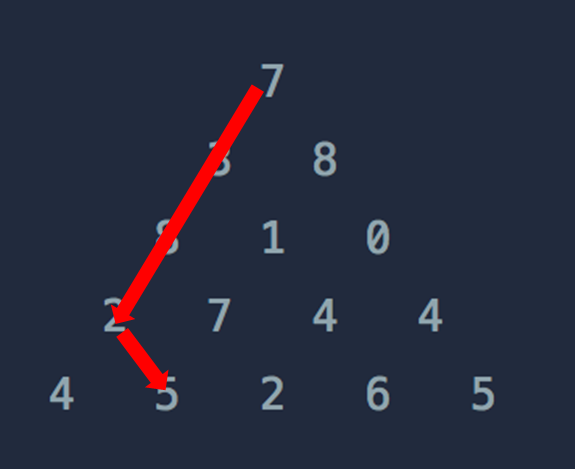
그러면 위에서부터 쭉 내려와서 하나 계산
또 쭉 내려와서 하나 계산
이렇게 계~~~~속 할 거란 말이에요.
그러면 뭐가 문제냐!
시간 초과?
맞죠!
근데 왜 시간 초과가 나는가 하면
중복된 연산이 계속 반복 되고 있기 때문입니다.
첫번째 사진과 두번째 사진을 보면
마지막의 숫자가 하나 다른 걸로
맨 위에서 부터 다시 내려오죠?
그렇게 중복된 연산이 반복되니까 시간이 많이 걸린다~~~~
그러면 어떻게 해야한다?
중복된 연산을 줄여야 한다.
그래서 위에서부터 내려오면서
가장 최적의 경우를 확인하면서 내려오자 이겁니다.
저 위에꺼는 제가 처음에 풀면서
좀 복잡하게 푼 거여서
다른 소스를 봅시다.
class Solution {
public int solution(int[][] triangle) {
int answer = 0;
int N = triangle.length;
int M = triangle[N-1].length;
for(int i = 1; i < N; i++){
triangle[i][0] += triangle[i-1][0];
triangle[i][i] += triangle[i-1][i-1];
for(int j = 1; j < i; j++){
triangle[i][j] += Math.max(triangle[i-1][j-1], triangle[i-1][j]);
}
}
for(int i = 0; i < M; i++){
answer = Math.max(answer, triangle[N-1][i]);
}
return answer;
}
}
맨 처음, 즉 맨 위의 값은
무조건 본인이 최적이니까
그 다음칸 부터 봅시다.
내가 봐야하는건 내 왼쪽 위, 내 바로 위의 값 중 큰 값이 무엇인지 입니다.
그런데 배열의 첫번째, 맨 마지막에 위치하는 애들은 좀 달라요.
첫번째 애는 자기 바로 위의 값도 가장 첫번째 값이에요.
그러니까 왼쪽 위가 없죠?
그러니까 맨 처음값은 항상 본인의 위의 값이 최대값이 되는 겁니다.
마지막 애는 자기 위의 값이 없죠?
배열이 밑으로 갈수록 하나씩 길어지니까요.
그러니까 항상 왼쪽 위의 값이 최대값이 됩니다.
그 외에, 그러니까 맨 처음과 맨 끝 사이 애들은
이제 좀 따져봐야 합니다.
어떤 애들을?
본인의 왼쪽 위와 바로 위의 값 중 어느게 더 큰 값인지!
그래서 더 큰 값을 본인의 값과 더 하면
그 위치까지 갈 때의 최대값이 된다~~~
그렇게 해서 쭉 구하고나면
이제 마지막 줄을 보면
거기에 도달하기 위한 방법 중
가장 큰 값이 저장되어 있습니다.
그 중에서 가장 큰 값이 우리가 원하는 값이겠죠?
방법은 여러가지 있겠지만
저는 마지막 줄을 한 번 쭉 봐서
가장 큰 값을 반환해 주었습니다.
여기까지 봐주셔서 감사합니다 ㅎㅎ

'프로그래머스 > Lv.0' 카테고리의 다른 글
| 연속된 수의 합 -Python (0) | 2024.10.29 |
|---|---|
| 프로그래머스 > 옹알이(1) - Python, re.sub() (2) | 2024.10.26 |
| 코딩테스트 연습 > 연속된 수의 합 - JAVA (0) | 2023.01.17 |
| 코딩테스트 입문 > 가까운 수 - JAVA (0) | 2022.12.29 |
| 프로그래머스 > 코딩테스트 입문 > 소인수분해 - JAVA (0) | 2022.12.29 |

